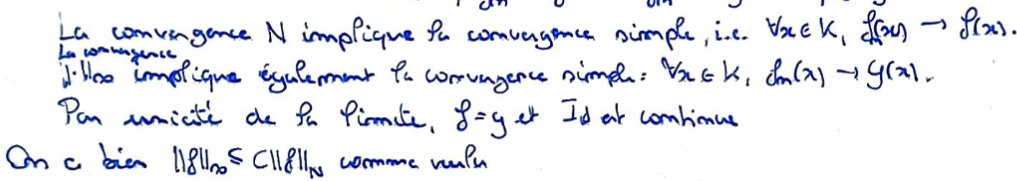Soit \(K\) un compact de \({\Bbb R}^d\) et \(N\) une norme quelconque sur \(\mathcal C^0((K,{\Bbb R}),N)\). On suppose que :
- \((\mathcal C^0(K,{\Bbb R}),N)\) est complet
- pour toute suite de \((f_n)_{n\in\Bbb N}\) qui converge dans \((\mathcal C^0(K,{\Bbb R}),N)\) vers une limite \(f\), on a \((f_n)_{n\in\Bbb N}\) qui converge simplement vers \(f\) sur \(K\).
Montrer que la norme \(N\) est équivalente à la norme infinie.
D'après le Théorème d'isomorphisme de Banach, on n'a besoin que d'une seule majoration.

On veut montrer que l'identité entre la norme \(N\) et la norme \(\lVert\cdot\rVert_\infty\) est continue par le Théorème du graphe fermé.
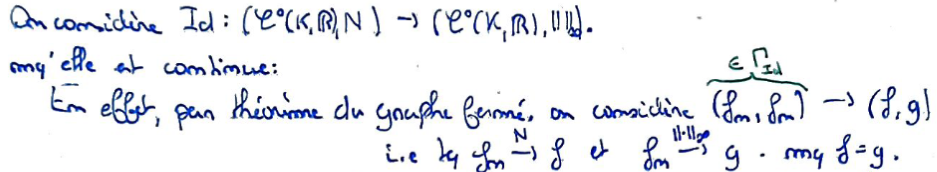
Pour cela, on utilise le fait que la convergence pour ces deux normes implique la convergence simple, et on conclut par unicité de la limite.